Digital Imaginging
How We Perceive Color
I have always loved the ability to take photos, even more so with the added capabilities that digital photography offers.
While I appreciate the art of photography, that is not what fascinates. As an engineer what I find most fascinating is the process of converting something we see with our eyes into a representation of numbers that can be used to recreate an approximation of what we saw. I think of my photography as more journalism than art - my main interest is usually to tell a story. While I can appreciate the artistic value of many techniques, and experiment with them from time to time to obtain different effects, I think I would easily become bored if that were all I did. But my heart beats faster when it comes to trying to capture a story or a unique scene, perhaps (or especially) with difficult lighting. The details of taking photons, converting them to numbers, and then recreating an image that bears a passable resemblence to what I saw is what I find most fascinating.
As I've spent a lot of time thinking about this, I thought I'd share some of the things I have learned. Even if the details of the image sensors and mathematical calculations don't interest you, having a basic understanding of how things work can be useful even if you are only interested in photography for art. So this will likely be the first of several posts.
Probably most of us learned way back in grade school that the "primary colors" are red, blue and yellow, and from those you could create other colors by mixing primary colors. If you ever think about that, you may be confused to see digital imaging devices discussed as RGB (red/green/blue). There are two things your grade school probably missed telling you - first of all, your red/blue/yellow "Primary Colors" are subtractive primary colors (used for mixing paints and pigments). The second is that the true subtractive primary colors are not red/blue/yellow, but magenta/cyan/yellow. Magenta is close to red, and cyan is close to blue, but they are not the same. Most digital devices (monitors, smart phone and camera screens, projectors and so on) are additive devices. That is, unlike pigments, which subtract color from white light, a monitor starts with zero light and then emits the additive primary colors in various combinations. We'll come back to this.
Another of those things you learned back in grade school is that "white light" (that is, sunlight), consists of all visible colors combined. This is where you were introduced to the prism/spectrum to see the "white" sunbeam broken up into a rainbow of color.
Most often, when color is discussed, it will be in terms of "mixing" colors, which tends to be misleading. If you have the impression that taking red light and green light and "mixing" them will result in a new light with the wavelength of yellow, then you have fallen victim to this idea of "mixing". If you "mix" red and green light, you will still have red and green light, both of which are unchanged. So how do we get yellow out of that combination? The answer is in how our eyes perceive light.
The "sensors" in our eyes are not capable of seeing all the different colors of the spectrum. Our eye sensors are Rods (which perceive light and dark, but not color) and Cones, which give us color information. There are 3 types of Cones, each of which is only sensitive to one predominate color. Those colors, as you may have guessed by now, are red, green, and blue. Each of them is sensitive to a range of frequencies around those "primary" colors, but it is a limited range. The figure below shows the frequency sensitivity of the different cones in a normal person's eye. While, say, the green sensor is sensitive to a range of colors that are centered on green, the brightness of all the colors it is sensitive to combine into a single signal from that sensor. What the brain receives are signals from 3 overlapping sensors, from which it builds an internal representation of a color that our mind sees.
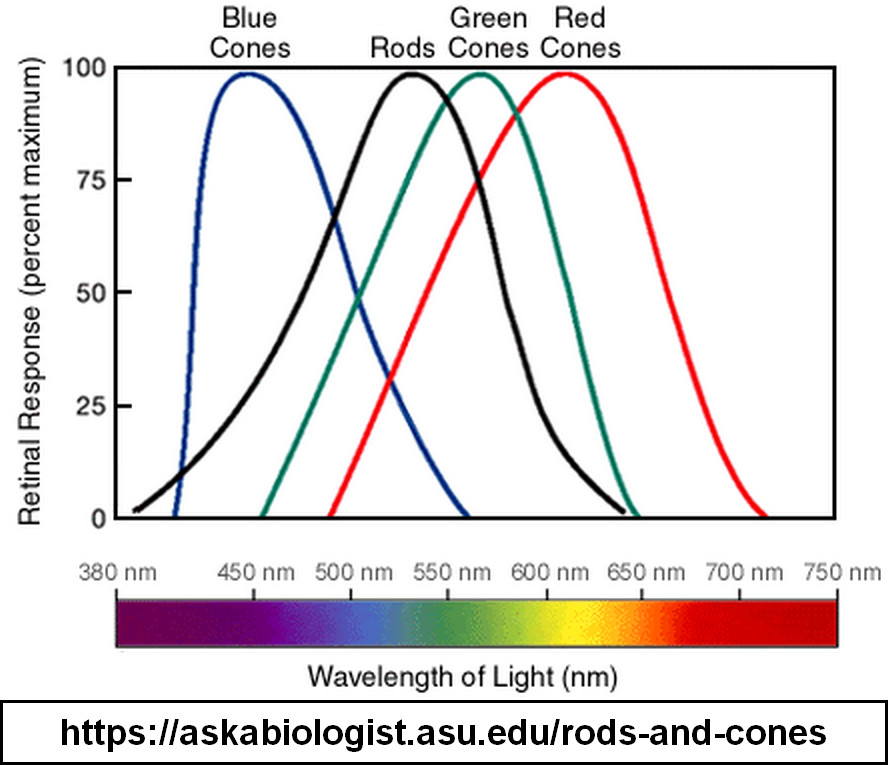
This shows the sensitivity of each of the three sets of cones in the eye of a person with normal vision. Each of the cones can only produce an intensity "signal" which varies with wavelength. Take the green cones for example: any light at the green wavelength (~560 nm) will register as a strong signal. However, light at ranges from blue to orange will cause some signal. The signal that is sent to the brain from the green cones is just a summation of the responses of all the colors from blue to orange. That signal has no information to divide up the values within the range of frequencies that cone was sensitive to. That is, a given level or blue or orange light would produce approximately the same signal level. It is the combination of the signals from each of the three cones that allow our brain to process a color. So, in order to reproduce color in a digital image, it is only necessary to recreate three distinct narrow-band colors - blue, red, and green, each of which is centered at the respective cone's peak response. As long as the level of that single color generates the same signal in our cones as the summation of all the signals in the range of cone sensitivity in the original image, our eye/brain cannot tell the difference. Also notice that the color yellow lies right between the peak sensitivity points of the red and green cones. Thus yellow is perceived from strong responses from two cones simultaneously, which is why it appears to be such a bright color.
By illuminating the red and green pixels we have not created the color yellow. What we are doing instead is playing a trick on our eyes - by shining red and green light into our eye in the same proportions that our rods and cones would have measured if the light had truly been yellow, our brain cannot tell the difference. If another creature had eyes that could detect yellow directly, they would likely be confused by our thinking that red and green on a computer screen are the color yellow.
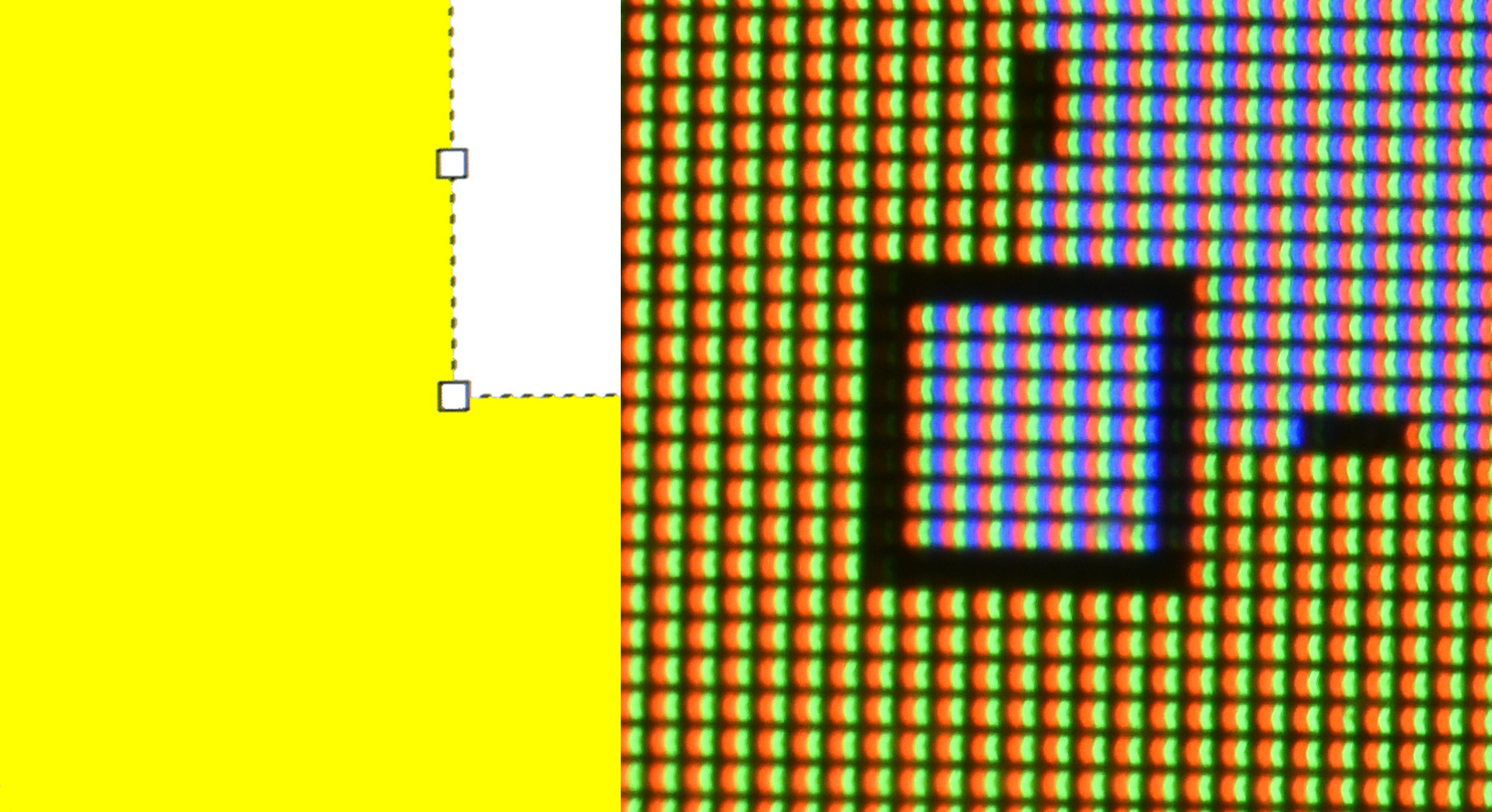
This is two views of a monitor, both showing the lower left corner of a white square on a yellow background. On the left is what our eye normally sees when viewing the monitor. On the right is a photograph of that same area of the screen with a close-up macro lens. This makes it clear that we are not actually seeing yellow light, but individual red and green light dots. The "white" area is not actually white - just equal levels of red, green, and blue light. Because all three different cones in our eyes are excited equally, we think we are seeing full spectrum white light.
The next figure shows the "digital image spectrum" compared to the white light spectrum. To our eyes, either one will appear to be white light. Because we can fool our eyes/brain like this, it becomes much simpler to record an image. A digital camera sensor uses individual sensors (pixels) that measure the strength of either red, green, or blue light, and then stores the levels of those 3 signals to record the color of a point of light. Those stored signals are then used to illuminate red green and blue pixels on a monitor to the same levels that were measured, and our eye/brain is tricked into "seeing" the full spectrum of color, even though all it is seeing is various levels of red, green and blue. To a device or creature that is truly capable of seeing all the colors in the visible light spectrum, our beautiful photos may not make much sense.

Our digital image light spectrum is only a subset of the white light spectrum. Because those three narrow-band colors (blue, green, red) excite the three sets of cones in our eyes equally, our brain is tricked into seeing no difference between the full white light spectrum and our discrete frequency digital image spectrum.
So this brings us to the heart of a digital image, which is nothing more than a grid of sets of measurements. Each tiny square in that grid is a "pixel", and it consists of 3 values for the measured signals of the red, green and blue channels. In the digital world information is stored in bytes, each byte being 8 bits, where a bit can have a value of zero or one. An 8-bit byte can have 256 different values, ranging from 0 to 255. Thus a full color pixel will consiste of 3 bytes, where each byte ranges from 0 to 255 for either red, green, or blue.
See the RGB gradation figure included with this post. That shows all of the possible values between 0 and 255 for each of the 3 individual color pixels, and for all 3 at the same level (the gray scale). Note that it is not possible to notice discrete steps in color - they all seem to be smooth gradations. That is because our eye is not capable of seeing more than 256 individual steps between dark and full bright, and may well see fewer. With 256 possible values for each of the 3 RGB colors, that gives us a total of 256-cubed possible colors, or a bit over 16 million. Various estimates have that our eyes can distinguish from several million to upwards of 10 million different color combinations, which all fall short of our 16 million color monitors.

This is the digital image color space. Each color pixel consists of three bytes - one each for red, green, and blue. An 8-bit byte contains 256 possible values, from 0 to 255. The lower bands of this figure shows all 256 values for all three bytes, from zero to 255. Our eye cannot distinguish any boundary between these values, and it appears to be a continuous gradation. For a final image then, 256 values for each of the three primary additive colors are all we need, and perhaps a bit more. If you consider all possible combinations of the three 256-value colors, that is 256-cubed, or a bit over 16 million possible color combinations. Estimates of the number of colors that can be perceived by a healthy eye range from several million up to around 10 million, all short of the 16 million possible combinations. The gray scale band at the top of this figure is created by equal levels of all three colors simultaneously.
As a final bit for this post, let's return to the Primary Colors we learned in grade school. This last figure shows two sets of Primary Colors - the additive and subtractive. Since we've been discussing monitors and digital cameras, which use the additive spectrum, we'll start with that. Instead of starting with white light, our monitors are black, and they create light from various pixels at different levels. As discussed above, when our eye detects red and green at equal levels, our mind sees yellow. Similarly, equal levels of green and blue become visualized as cyan, and red and blue become magenta. All three combined are perceived as white (in the center).
Now, we go to the subtractive spectrum, and we see that the subtractive primary colors are the colors we just created by combining two of the additive primary colors - that is, yellow, cyan, and magenta. But recall that subtractive colors work by interacting with white light. Thus we may think of yellow as the result of subtracting blue from the white light specturm, leaving red and green. Similarly, magenta, created by combining red and blue light, may be thought of as subtracting green from white light. And cyan, consisting of blue and green light, acts to subtract red from the white light spectrum. Each of the primary subtractive colors effectively removes one of the three primary additive colors. All three added together result in black. You'll probably recognize that yellow, cyan and magenta are the colors of your inkjet or color laser printer ink/toner. For practical reasons, black is used as a fourth ink color as it is easier to get a true crisp black directly than by mixing the three other colors.
So, remember from grade school how blue and yellow made green? Substitute cyan for blue, and recall that cyan subtracts red. Yellow subtracts blue. So, having subtracted red and blue from the white light (or, to our eyes, the RGB) spectrum, what we have left is green.
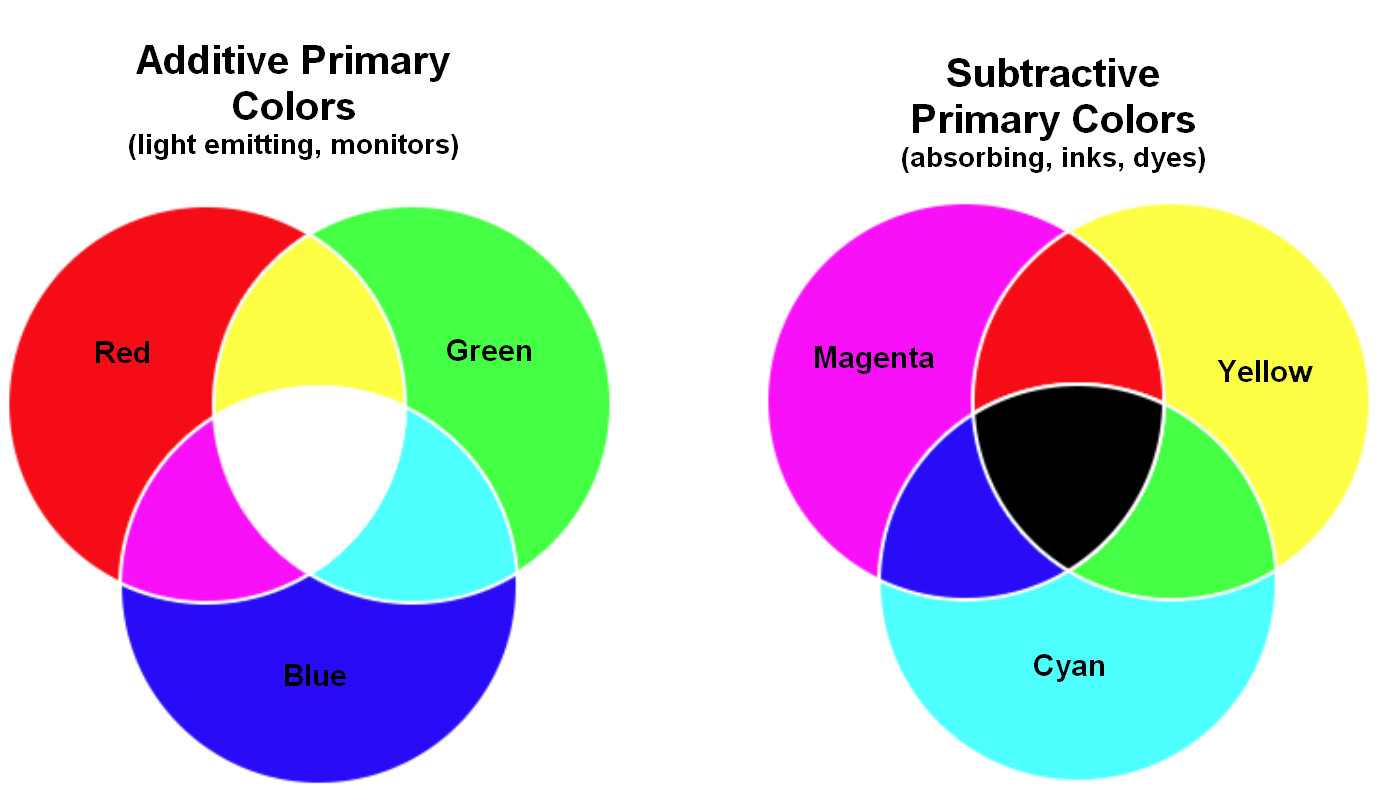
This shows the two sets of primary colors. Our digital imaging devices (monitors, smartphones, camera screens) use the additive primary colors. That is, the default value is black, and light is added at one of the three primary wavelengths. Other colors are created by combining the three primary colors. Thus yellow = red + green; cyan = green + blue; magenta = red + blue. All three combined equally produce what our eye interprets as white. The subtractive primary colors are used for inks and toners for our printers. They presume we are starting with white light illumination, and then subtract light at specific wavelengths from the white light spectrum. From the additive spectrum we see that yellow=red+green light, so yellow ink has the effect of removing blue from the full white light spectrum. Similarly, cyan (green+blue) removes red, and magenta (red+blue) removes green. As an example of how this works: if you combine cyan (which removes red), with yellow (which removes blue), you end up with only green remaining - a result likely familiar from color mixing in grade school. And finally, combining all three subtractive colors results in black, as there is no light left. As a practical matter, our printers add black ink as a way of achieving this lack of color directly, rather than by a combination of the three colored inks.
This is just a broad brush on how we see and record color. In truth, there are some colors that our eyes can see that a digital device cannot recreate, and different digital devices do better at expressing the full ranges of values than others. These differences are described by various color gamuts, which is another term for range. But those are at the edges of our visible color space, and a more advanced topic than I am covering here.