Effect of FLPHG Engine Thrust on Bar Position
Most flphg pilots are familiar with the
apparent change of control
bar position when using a powered harness. Nothing about the
glider changes, rather the pilot now has additional weight located
below the feet. In order to balance pilot and engine, the harness
suspension point must be moved to the rear, which effectively moves the
glider forward with respect to the glider. See
Illustration of Control Bar Position Change
for clarification if you are still unclear on this point. Up to
this point we are not considering the engine - that is only the weight
distribution of the harness, with the engine off.
Adding Thrust
This is where the picture becomes less clear for many. What
happens to bar position when you start the motor and add the prop
thrust to the picture?
Before going on, think about this for a
moment first. Does the bar (relative to the pilot) move back,
stay in the same place, or move forward? Does the glider speed
up? What happens to sink/climb rate?
The Basics
For this discussion the pilot will apply no pitch pressure - that
is, the pilot is flying at the glider's trim position. This is
not a limitation, simply a way of removing some variables from the
equation. The glider can be trimmed at any speed - min sink, best
glide, top speed, etc. But we will always let the glider
determine the pitch angle, with no bar pressure applied by the pilot.
In addition to the aerodynamic forces on the wings, there are two other
forces which act on a hang glider: the weight of the glider, and
the force in the hang strap.
Note that I did not say the pilot's weight. Think about a pilot
at the top of a loop - the glider knows
nothing about the pilot's weight, only the force in the hang
strap that is attached to the pilot. As long as the strap is in
tension, the glider continues flying around the loop.
The glider could care less about gravity or what is right side
up. It will attempt to return to a stable flying angle of attack
relative to the direction of the forces acting on it. A glider
would be perfectly happy flying upside down or straight up, if the
forces acting on it were in the right direction.
Think about a kite - it has the same two forces acting on it - the
weight of the kite, and the tension in the string. It can
fly at many heights and angles to the ground.
The Forces on a Glider
Of course we have aerodynamic forces (lift and drag), but they are
only
present when other forces cause the glider to move relative to the
air. And those other forces are the glider weight and hang strap tension, as shown in the figure.
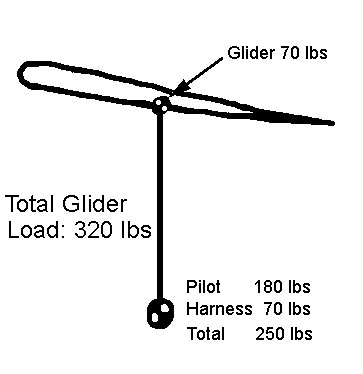
I'll pick round numbers for all the weights:
Glider - 70 lbs (this probably
includes a fuel tank mounted on the top
of the downtubes)
Pilot - 180 lbs
Harness - 70 lbs (this includes
parachute, etc)
Flying along, power off, there is therefore a 250 lb load in the hang
strap. The
total load being
borne by the glider is 320 lbs.
We are looking only at level flight, no turns, so this total load is
acting straight down. The pilot is letting the glider fly at
trim, as we already mentioned, so there is no pitch pressure.
CG Locations
The Center of Gravity (CG) of the pilot must be directly below the hang
point for this case. We are going to assume that the CG of the
glider is at the hang point. This is a reasonable approximation,
although it may actually be slightly above or below it.
Now Add Thrust to Hang Strap Load
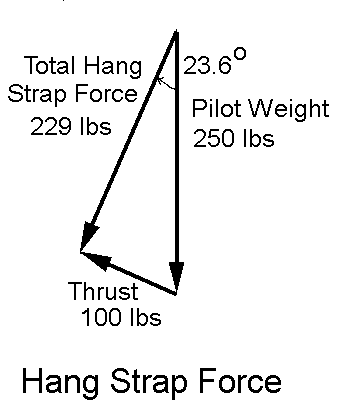
Now, let's add prop thrust to the picture.We are going to
keep this simple and assume that the pilot is hanging perfectly level
with the engine off (although many pilots actually fly with the tail of
the harness a bit lower than the head). This means that the pilot forms
a 90 degree angle to the hang strap. We are also going to use
a nice round number of
100 lbs of
thrust.
The thrust pushes the pilot forward, and this causes the pilot,
harness, and hang strap to rotate about the hang point, as shown in the
figure to the left. The thrust vector and the hang strap maintain the
90 degree angle that existed with power off. Note that the
total force in the hang strap has
decreased, to
229 lbs.
Does this make sense? Sure - think about the harness tail
pointing straight down - sort of like an upside down helicopter - in
that case the thrust would subtract directly from the pilot's weight.
Also notice the hang strap angle
is 23.6 degrees from vertical. If we looked only at this
figure, we would conclude that the pilot has moved a long ways forward
through the control bar. In fact, we can use the figure and
numbers at left to figure out just how far. Let's say the pilot
CG is 50 inches below the hang point - then we can use the figure at
left by simply dividing all
the numbers by 5. The Pilot Weight Vector would now be 50, which
is his distance below the hang point. The Thrust vector would now
be the distance the pilot has moved forward, which would be 20 inches! But
this can't be right, because that is as long , or longer, than most
people's arms. But this is assuming the glider has not
changed position at all, which is obviously not the case.
Total Glider Load
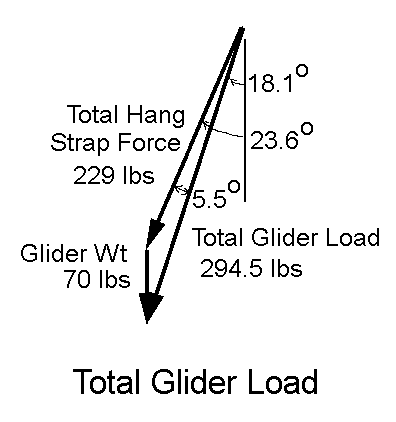
Now we can take a look at the whole picture. I've
taken the Hang Strap Load vector from the previous figure and copied it
to the figure at the left. To this I've added the Glider Weight
Vector. This is, of course, assuming steady state, non-turning
flight. We now see that the
Total
Load on the Glider is 294.5 lbs, and the angle from the
vertical at which it acts.
That's it - that one quantity, the
Total Glider
Load, is all that the glider knows.
The glider does not
know
anything about gravity, engine thrust, or any of the other values we
used to get to this point. The glider will fly based solely on
that one load vector.
Now, let's look at what we can conclude from that.
1.
The glider will fly exactly the
same as if it had a total load of
294.5 lbs on it. Forget about the thrust and everything
else - we
now just have a glider with a total load of 294.5 lbs, instead of the
320 lbs we saw earlier.
So
the glider will be flying slightly slower (remember that the
velocity change is only the square root of the weight change). It
will also
have
exactly the same angle,
relative to the total load, that it has
unpowered. So, because the angle of the total load has
changed,
so will the glider pitch angle. That is, in our example, the
glider will be pitched up by 18.1 degrees. But the glider does
not know it is pitched at a higher angle, as far as it is concerned, it
is flying exactly the same as if it were unpowered and flying with a
294.5 lb total weight.
2. Now let's look at what the pilot is experiencing. Remember
that the
pilot is angled
23.6 degrees forward from the hang point. But the
glider control bar has angled up
18.1 degrees. So the
pilot has an
angle, relative to the glider, of only 5.5 degrees.
If we continue to use the hang strap length of 50 inches, then this
means the
pilot has moved
4.8 inches further forward than the control bar has. (simply
muliply the strap length by the rotation angle, in radians).
Summary and Conclusions
When we take all the above pieces and put them together, this is what
we get:
1. The glider responds only to the Total Load Vector acting on it.
2. Adding thrust to the pilot changes the angle of the hang strap
tension load, and slightly reduces the tension from when the power was
off.
3. The total load on the glider is reduced, and angled forward.
The glider will continue to fly at the same angle, relative to the
Total Load Vector, that it did before, but at a slightly slower
speed.
4. Because the glider weight and hang strap tension loads are in
different directions, under power, the control bar position relative to
the pilot will change. The
heavier the pilot, and the lighter the glider, the less change in
control bar position there will be. Conversely, the lighter the
pilot and the heavier the glider, the more change will be experienced.
We can use this information to make an approximate Rule of Thumb:
Approximate Rule of Thumb:
Changing thrust
changes sink/climb rate, changing bar position changes speed. As we have seen,
changing thrust also changes speed and bar position slightly, but not
by much. If a pilot changes the bar position, he changes the
speed. The effect, on the glider, of pulling in or pushing out on
the control bar is no different from simply moving the hang point
forward or aft. In the first case the pilot must maintain the bar
at the new position by exerting a force on it, in the second case the
glider trims at the new speed with no bar pressure. The
difference in bar pressure between those two cases is the only
difference there is, and the glider does not know which of those two
cases it is responding to. Now, changing speed will also change
the sink/climb rate, but not by nearly as much as the speed
changes. So, to a first approximation, the rule of thumb above
works very well for thinking about how the glider responds to the two
control inputs of throttle setting and control bar position.